Προτάσις A' - Proposition the First
-Upon A Given Straight Line Segment An Equilateral Triangle Is To Be Constructed-
-Upon A Given Straight Line Segment An Equilateral Triangle Is To Be Constructed-
Let a given straight line segment be called AB.
And so, it is necessary that upon the straight line segment AB an equilateral triangle is constructed.
At point A, let a circle BCD be inscribed with radius AB...
...and from point C, where the circles intersect each other, let straight lines CA and CB be joined to points A and B.
And since point A is the center of circle CDB, line segment AC is equal to AB.
Again, since point B is the center of circle CAE, line segment BC is equal to BA.
And now is it also shown that line segment CA is equal to AB. Therefore, each of the line segments, CA, CB, and AB are equal, and things which are equal to the same thing are also equal to each other. And line segment CA is thus equal to CB. Therefore these three segments, CA, AB, and BC are all equal to each other.
Therefore the triangle ABC is equilateral, and it hath been constructed upon the given straight line segment AB.
-Upon A Given Straight Line Segment An Equilateral Triangle Has Been Constructed-
THE VERY THING WHICH HAD TO BE DONE
Notes:
Points D & E lie somewhere on the circumference of circles CDB & CAE respectively. They are mentioned to help define their respective circles.
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις B' - Proposition the Second-
-At A Given Point A Straight Line Segment Equal To A Given Straight Line Segment Is To Be Drawn-
Let a given point be named A, and a given straight line segment BC.
And since point B is the center of circle CGH, line segment BC is equal to BG.
Again, since point D is the center of GKL, line segment DL is equal to DG, and of these DA is equal to DB. Therefore, the remainder AL is equal to the remainder BG.
And now is it also shown that BC is equal to BG.
Therefore, each of the line segments AL, BC, and BG are equal, and things which are equal to the same thing are also equal to each other.
And therefore AL is equal to BC.
-And Therefore, At Given Point A The Straight Line Segment AL Is Drawn Equal to The Given Straight Line Segment BC-
THE VERY THING WHICH HAD TO BE DONE
Let there be set at point A a line segment AD equal to straight line C (found using Proposition 2, and therefore, also 1).
[Unnecessary Prop. 1 aids will now be discarded.]
[Unnecessary Prop. 2 aids will now be discarded.]
And, making the center at point A, let a circle with the radius AD be drawn, called circle DEF.
-And Therefore, From Two Unequal Straight Line Segments, AB and C, From The Greater Straight Line Segment AB A Line Segment Equal To the Lesser Line Segment C Is Cut-
THE VERY THING WHICH HAD TO BE DONE
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις Γ' - Proposition the Third-
-Given Two Unequal Straight Line Segments, To Cut Off From The Greater A Straight Line Segment Equal To The Less-
Let there be given two straight line segments of unequal length, named AB and line C, of which let the greater be AB.
And so, it is necessary to cut off from the greater line segment AB a straight line segment equal to shorter line C.
Let there be set at point A a line segment AD equal to straight line C (found using Proposition 2, and therefore, also 1).
And since point A is at the center of circle DEF, line segment AE is equal to line segment AD.
But also, line C is equal to line segment AD.
And therefore, concerning line segment AE, C is equal to AD, and so AE is also equal to C.
And therefore, concerning line segment AE, C is equal to AD, and so AE is also equal to C.
THE VERY THING WHICH HAD TO BE DONE
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις Δ' - Proposition the Fourth-
-If Ever Two Triangles Have Two Sides Equal To Two Sides Respectively While Having The Angles Contained By The Equal Straight Line Segments Also Be Equal, Then The Base Of One Is Equal To The Base Of The Other, And The One Triangle Will Be Equal To The Other Triangle, And The Remaining Angles Will Be Equal To The Other Triangle's Remaining Angles Respectively At The Place Where the Equal Sides Subtend-
Let there be two triangles called ABC and DEF...
...having two sides AB and AC equal to the sides DE and DF of the other triangle respectively, so that AB is to DE and AC is to DF...
...and the angle at BAC is equal to the angle at EDF.
I say that the base BC of the one triangle is equal to base EF of the other, and triangle ABC is equal to DEF, and the remaining angles will be equal to the other triangle's remaining angles respectively at the place where the equal sides subtend, namely...
...the angle at ABC to the angle at DEF, and the angle at ACB to the angle at DFE.
For if triangle ABC were fitted onto triangle DEF, and point A is placed upon point D, and straight line segment AB placed upon DE, and then point B will fit upon E, because straight line segment AB is equal to DE. Indeed, with AB fitted on DE, and straight line segment AC will fit upon DF because the angle at BAC is equal to the angle at EDF.
Hence, point C will fit upon point F because line segment AC is equal to DF, but then also point B had fitted to E.
Hence, the base BC will fit upon the base EF. For, if in fitting point B upon point E and point C upon point F so that base BC will not fit upon EF, then the two straight line segments will enclose a space -- this very thing is impossible.
Therefore, base BC will fit upon EF and be equal to it.
And so the whole triangle ABC will fit upon the whole triangle DEF and be equal to it, and the remaining angles will fit upon the other triangle's remaining angles and be equal to them, namely, the angle at ABC to the angle at DEF, and the angle at ACB to the angle at DFE.
For if this were possible, then from the ends of line segment AB let two straight line segments AC and CB extend to point C and form a triangle...
...while let straight line segments AD and DB, equal to AC and CB respectively, extend from the ends of AB as well, but meet at point D, a different point than C, namely so that CA equals DA and has the same end A, and CB equals DB and has the same end B.
Let the two points C and D be joined by straight line segment CD.
So, since AC is equal to AD, angle ACD must be equal to angle ADC (via Proposition 5).
And therefore, angle ADC must be greater than angle DCB. And therefore, angle CDB is much greater than DCB (keeping in mind that, if this is possible, angle ACD must be equal to angle ADC).
Again, since CB is equal to DB, angle CDB must be equal to DCB (again, via Proposition 5).
But it has been demonstrated that angle ADC is already much greater than angle DCB -- which is an impossibility.
Let there be two triangles, ABC and DEF...
...where the two sides AB and AC are equal to the two sides DE and DF respectively, namely that AB is equal to DE and AC to DF. Let the base BC equal to base EF. I say that the angle at BAC is equal to the angle at EDF.
For if in fitting triangle ABC upon triangle DEF and setting point B upon point E and straight line BC upon straight line EF, then point C will fit upon point F because BC is equal to EF.
Indeed, if BC is fitted upon EF, then sides BA and CA will fit upon ED and DF.
But if the base BC fits upon the base EF, and sides BA and AC do not fit upon sides ED and DF, but instead lie beside them as sides EG and GF, then that means that two straight lines must be constructed from the ends of the base equal to the already given straight lines respectively; and these straight lines must meet to form a triangle, but at a different point from the other triangle -- but no such triangle can be formed (via Proposition 7).
And therefore, it is not possible that in fitting the base BC upon the base EF, the sides BA and AC will not fit upon sides ED and DF respectively. The result of this is that the angle BAC will fit upon and be equal to angle EDF.
Let there be a given rectilinear angle BAC. So, it is necessary to bisect this angle.
Let point D be chosen at random along line AB...
...and let AE be cut off from AC and made equal to AD.
Then let DE be joined...
and upon DE let an equilateral triangle DEF be constructed.
Then, let be joined AF.
I say that the angle BAC has been bisected by the straight line AF.
For since AD is equal to AE and AF is common between them, then the two sides DA and AF are equal to the sides EA and AF respectively...
...and the base DF is equal to the base EF. And therefore, the angle DAF is equal to the angle EAF.
Let there be a given infinite straight line AB and a given point C which does not lie upon the line.
It is necessary to draw a perpendicular straight line upon this given infinite straight line AB from the given point C which does not lie upon it.
For let point D be taken at random from the other side of the straight line AB...
...and, with point C in the center and line CD being the radius, let circle EFG be drawn.
And let straight line EG be bisected at point H...
...and let sides CG, CH, CE be joined.
I say that straight line CH has been drawn perpendicular to given infinite straight line AB from point C which does not lie on it.
For since GH is equal to HE, and GC is common between them, then the two sides GH and HC are equal to the two sides EH and HC respectively, and the base CG is equal to the base CE.
And therefore, angle CHG is equal to EHC, and they are adjacent.
And whenever a straight line set upon another straight line makes angles equal to each other, then either of the angles is a right angle, and the one set up upon the other is said to be perpendicular to the line upon which it stands.
For let any straight line segment be made named AB and let it be set up upon another straight line segment CD...
...such that it makes angles CBA and ABD.
I say that the angles at CBA and ABD are both right angles or equal two right angles (and thus make 180°).
So, if the angle at CBA is equal to the angle at ABD, then the two are right angles.
But if not, then let be led from point B straight line BE at right angles to straight line CD
I say that angle AEC is equal to angle DEB, and angle CEB to angle AED.
For since straight line AE stands upon straight line CD, thus making angles CEA and AED, therefore, the angles CEA and AED are both equal to right angles. Again, since straight line DE stands upon straight line AB, thus making angles AED and DEB, therefore angles AED and DEB are both equal to right angles. And both angles CEA and AED have been demonstrated to be equal to right angles -- therefore, angles CEA and AED are equal to AED and DEB. Let the common angle AED be removed: the remaining angle CEA is equal to the remaining angle BED, and likewise shall it be demonstrated that also angle CEB and DEA are equal.
Let AC be bisected (Prop. 10) at point E...
And let straight line FC be drawn, connecting points F and C, and let straight line AC be drawn out to point G.
And so, since AE is equal to EC, and BE to EF, then the two straight lines AE and EB are equal to CE and EF respectively. And the angle AEB is equal to angle FEC, for they vertically opposite.
Therefore, the base AB is equal to FC, and triangle ABE is equal to triangle FEC, and the remaining angles of one triangle are equal to the other triangle's remaining angles respectively, where the equal sides subtend.
Therefore, angle BAE is equal to angle ECF. The angle at ECD is greater than the angle ECF -- therefore, the angle ACD is greater than BAE; similarly, if BC be bisected, the angle BCG, which is in essence the same as angle ACD (via Prop. 15), is greater than ABC.
Hence, point C will fit upon point F because line segment AC is equal to DF, but then also point B had fitted to E.
Hence, the base BC will fit upon the base EF. For, if in fitting point B upon point E and point C upon point F so that base BC will not fit upon EF, then the two straight line segments will enclose a space -- this very thing is impossible.
Therefore, base BC will fit upon EF and be equal to it.
And so the whole triangle ABC will fit upon the whole triangle DEF and be equal to it, and the remaining angles will fit upon the other triangle's remaining angles and be equal to them, namely, the angle at ABC to the angle at DEF, and the angle at ACB to the angle at DFE.
-And Therefore, if ever Two Triangles Have Two Sides Equal To Two Sides Respectively While Having The Angles Contained By The Equal Straight Line Segments Also Be Equal, Then The Base Of One Is Equal To The Base Of The Other, And The One Triangle Will Be Equal To The Other Triangle, And The Remaining Angles Will Be Equal To The Other Triangle's Remaining Angles Respectively At The Place Where the Equal Sides Subtend-
THE VERY THING WHICH HAD TO BE DEMONSTRATED
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις E' - Proposition the Fifth-
-Concerning Isosceles Triangles, The Angles At The Base Are Equal To Each Other, And If The Equal Straight Lines Be Drawn Out Further, Then The Angles Underneath The Base Will Be Equal To Each Other-
Let there be an isosceles triangle called ABC having one side AB equal to side AC...
...and should straight lines BD and CE be drawn out further from AB and AC...
...then I say that the angle at ABC is equal to the angle at ACB, and the angle at CBD is equal to the angle at BCE.
For let be taken at random from line BD point F...
....and let line segment AG be taken from the greater line AE and made equal to the smaller line AF (found using Proposition 3)...
...and let be joined together straight lines FC and GB.
And so, since line AF is equal to AG and AB to AC, then yea, the two lines AF and AB are equal to lines AG and AC respectively, and the two lines FA and AC are equal to lines GA and AB respectively, and they have a common angle at FAG.
Therefore, the base FC is equal to the base GB, and triangle AFC will be equal to triangle AGB, and the remaining angles of one triangle will be equal to the remaining angles of the other triangle respectively where the equal sides subtend, that is, the angle at ACF to the angle ABG, and the angle of AFC to angle AGB. And since the whole line AF is equal to the whole line AG, and of these, AB is equal to AC, then therefore the remaining line BF is equal to the remaining line CG.
It hath been demonstrated that FC is equal to GB; therefore, the two sides BF and FC are equal to the two sides CG and GB respectively. And the angle at BFC is equal to the angle CGB, and the base BC is common to them.
And therefore, triangle BFC will be equal to triangle CGB, and the remaining angles of one triangle will be equal to the remaining angles of the other triangle respectively where the equal sides subtend: therefore the angle at FBC is equal to the angle at GCB, and the angle at BCF is equal to CBG. Therefore, since the whole angle at ABG hath been demonstrated to be equal to the whole angle at ACF, and of these CBG is equal to BCF, then therefore, the remaining angle at ABC is equal to the angle at ACB; and these are at the base of the triangle ABC.
And it hath been demonstrated that the angle at FBC is equal to the angle at GCB, and these are under the base.
...and should straight lines BD and CE be drawn out further from AB and AC...
And so, since line AF is equal to AG and AB to AC, then yea, the two lines AF and AB are equal to lines AG and AC respectively, and the two lines FA and AC are equal to lines GA and AB respectively, and they have a common angle at FAG.
Therefore, the base FC is equal to the base GB, and triangle AFC will be equal to triangle AGB, and the remaining angles of one triangle will be equal to the remaining angles of the other triangle respectively where the equal sides subtend, that is, the angle at ACF to the angle ABG, and the angle of AFC to angle AGB. And since the whole line AF is equal to the whole line AG, and of these, AB is equal to AC, then therefore the remaining line BF is equal to the remaining line CG.
It hath been demonstrated that FC is equal to GB; therefore, the two sides BF and FC are equal to the two sides CG and GB respectively. And the angle at BFC is equal to the angle CGB, and the base BC is common to them.
And therefore, triangle BFC will be equal to triangle CGB, and the remaining angles of one triangle will be equal to the remaining angles of the other triangle respectively where the equal sides subtend: therefore the angle at FBC is equal to the angle at GCB, and the angle at BCF is equal to CBG. Therefore, since the whole angle at ABG hath been demonstrated to be equal to the whole angle at ACF, and of these CBG is equal to BCF, then therefore, the remaining angle at ABC is equal to the angle at ACB; and these are at the base of the triangle ABC.
And it hath been demonstrated that the angle at FBC is equal to the angle at GCB, and these are under the base.
-And Therefore, Concerning Isosceles Triangles, The Angles At The Base Are Equal To Each Other, And If The Equal Straight Lines Be Drawn Out Further, Then The Angles Underneath The Base Will Be Equal To Each Other-
THE VERY THING WHICH HAD TO BE DEMONSTRATED
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις F' - Proposition the Sixth-
-If Ever Two Angles Of A Triangle Are Equal To Each Other, Then The Sides Subtending Said Equal Angles Shall Be Equal To Each Other-
Let there be a triangle ABC having angle ABC equal to angle ACB.
I say that side AB is equal to side AC.
For if side AB were unequal to side AC, then one of them must be greater.
So let side AB be greater...
and let line segment DB be cut off from the greater length of side AB and made equal to side the smaller side AC (found using Proposition 3)...
...and then let side DC be made to join points D and C.
Therefore, since side DB is equal to side AC, and BC is in common between them, then rightly so the sides DB and BC equal sides AC and CB respectively...
...and the angle at DBC is equal to the angle at ACB (via Proposition 4, Side-Angle-Side).
And therefore, the base DC is equal to the base AB, and the triangle DBC is equal to ACB, with the smaller triangle being equal to the greater -- which is an absurdity.
And therefore, side AB is not unequal to side AC -- therefore, they are equal.
For if side AB were unequal to side AC, then one of them must be greater.
So let side AB be greater...
And therefore, the base DC is equal to the base AB, and the triangle DBC is equal to ACB, with the smaller triangle being equal to the greater -- which is an absurdity.
-And Therefore, If Ever Two Angles Of A Triangle Are Equal To Each Other, Then The Sides Subtending Said Equal Angles Shall Be Equal To Each Other-
THE VERY THING WHICH HAD TO BE DEMONSTRATED
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις Z' - Proposition the Seventh-
-Two Straight Line Segments Extending From Either End Of A Straight Line Segment To Form A Triangle Cannot Be Constructed So That Two Straight Line Segments Of Equal Length Can Extend From Either End Of The Same Straight Line Segment Towards Any Other Point-
For if this were possible, then from the ends of line segment AB let two straight line segments AC and CB extend to point C and form a triangle...
-And Therefore, Two Straight Line Segments Extending From Either End Of A Straight Line Segment To Form A Triangle Cannot Be Constructed So That Two Straight Line Segments Of Equal Length Can Extend From Either End Of The Same Straight Line Segment Towards Any Other Point-
THE VERY THING WHICH HAD TO BE DEMONSTRATED
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις H' - Proposition the Eighth-
-If Ever Two Triangles Have Two Sides Equal To Two Sides Of Another Triangle Respectively, And The Base Of One Triangle Is Equal To The Other Triangle's Base, Then The One Triangle Will Have The Angle Found Between The Extended Sides Equal To The Other Triangle's Angle-
Let there be two triangles, ABC and DEF...
For if in fitting triangle ABC upon triangle DEF and setting point B upon point E and straight line BC upon straight line EF, then point C will fit upon point F because BC is equal to EF.
Indeed, if BC is fitted upon EF, then sides BA and CA will fit upon ED and DF.
-And Therefore, If Ever Two Triangles Have Two Sides Equal To Two Sides Of Another Triangle Respectively, And The Base Of One Triangle Is Equal To The Other Triangle's Base, Then The One Triangle Will Have The Angle Found Between The Extended Sides Equal To The Other Triangle's Angle-
THE VERY THING WHICH HAD TO BE DEMONSTRATED
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις Θ' - Proposition the Ninth-
-To Bisect A Given Rectilinear Angle-
Let there be a given rectilinear angle BAC. So, it is necessary to bisect this angle.
-And Therefore, A Given Rectilinear Angle BAC Hath Been Bisected By Straight Line AF-
THE VERY THING WHICH HAD TO BE DONE
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις I' - Proposition the Tenth-
-To Bisect A Given Finite Straight Line-
Let there be a given finite straight line AB. Indeed, it is necessary to bisect this finite straight line AB.
Let be constructed upon this line equilateral triangle ABC...
...and let the angle ACB be bisected by the straight line CD. I say that straight line AB hath been bisected at point D.
For since AB is equal to CB, and CD is common between them, and indeed the two straight lines AC and CD are equal to the straight lines BC and CD respectively, and angle ACD is equal to BCD (via Proposition 4). And therefore, the Base AD is equal to the base BD.
-And Therefore, A Given Finite Straight Line AB Hath Been Bisected At Point D-
THE VERY THING WHICH HAD TO BE DONE
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις I'A' - Proposition the Eleventh-
-To Draw A Straight Line At Right Angles (90°) To A Given Straight Line At Any Given Point On It-
Let there be a given straight line AB...
...and a point given on the line at C. It is necessary to draw a straight line at right angles to a given straight line at any point on it.
Let be taken a point at random upon AC and call it D; then let CE be made equal to CD...
...and let an equilateral triangle be constructed upon DE called FDE.
Then let FC be joined.
I say that line FC hath been drawn at right angles to the given straight line AB from C, the given point on it.
For since DC is equal to CE and CF is common between them, then the two sides DC and CF are equal to the sides EC and CF respectively, and the base DF is equal to the base FE. And therefore, angle DCF is equal to angle ECF, and they are likewise adjacent. And whenever a straight line makes adjacent angles equal to each other upon a straight line, each of the angles is a right angle.
And therefore, either angle, DCF and FCE, are right angles.
Then let FC be joined.
I say that line FC hath been drawn at right angles to the given straight line AB from C, the given point on it.
For since DC is equal to CE and CF is common between them, then the two sides DC and CF are equal to the sides EC and CF respectively, and the base DF is equal to the base FE. And therefore, angle DCF is equal to angle ECF, and they are likewise adjacent. And whenever a straight line makes adjacent angles equal to each other upon a straight line, each of the angles is a right angle.
And therefore, either angle, DCF and FCE, are right angles.
-And Therefore, A Straight Line CF Hath Been Drawn At Right Angles To A Given Straight Line AB At C, The Point Given Point On It-
THE VERY THING WHICH HAD TO BE DONE
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις I'B' - Proposition the Twelfth-
-To Draw A Perpendicular Straight Line Upon A Given Infinite Straight Line From A Given Point Which Does Not Lie Upon Said Line-
Let there be a given infinite straight line AB and a given point C which does not lie upon the line.
It is necessary to draw a perpendicular straight line upon this given infinite straight line AB from the given point C which does not lie upon it.
I say that straight line CH has been drawn perpendicular to given infinite straight line AB from point C which does not lie on it.
For since GH is equal to HE, and GC is common between them, then the two sides GH and HC are equal to the two sides EH and HC respectively, and the base CG is equal to the base CE.
And therefore, angle CHG is equal to EHC, and they are adjacent.
And whenever a straight line set upon another straight line makes angles equal to each other, then either of the angles is a right angle, and the one set up upon the other is said to be perpendicular to the line upon which it stands.
-And Therefore, A Perpendicular Straight Line CH Hath Been Drawn Upon A Given Infinite Straight Line AB From A Given Point C Which Does Not Lie Upon AB-
THE VERY THING WHICH HAD TO BE DONE
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις I'Γ' - Proposition the Thirteenth-
-If Ever A Straight Line Being Set Up Upon Another Straight Line Creates An Angle, It Will Make Either Two Right Angles (180°) Or Two Angles Equal To Two Right Angles (180°)-
I say that the angles at CBA and ABD are both right angles or equal two right angles (and thus make 180°).
So, if the angle at CBA is equal to the angle at ABD, then the two are right angles.
But if not, then let be led from point B straight line BE at right angles to straight line CD
Therefore, the angles at CBE and EBD are both right angles. And since the angle at CBE is equal to the two angles at CBA and ABE, then let angle EBD be added in common (to each); therefore, the angles at CBE and EBD are equal to the three angles at CBA, ABE, and EBD. Again, since the angle at DBA is equal to the two angles at DBE and EBA, then let angle ABC be added in common (to each); therefore, the angles at DBA and ABC are equal to the three angles at DBE, EBA, and ABC. And the angles at CBE and EBD have also been demonstrated to be equal to the same three angles -- things which are equal to the same thing are also equal to one another. And the angles at CBE and EBD are therefore equal to the angles at DBA and ABC, but the angles at CBE and EBD are right angles. And the angles at DBA and ABC are therefore equal to two right angles.
-And Therefore, If Ever A Straight Line Being Set Up Upon Another Straight Line Creates An Angle, It Will Make Either Two Right Angles (180°) Or Two Angles Equal To Two Right Angles (180°)-
THE VERY THING WHICH HAD TO BE DONE
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις I'Δ' - Proposition the Fourteenth-
-If With Any Straight Line And At Any Point On Said Straight Line Two Straight Lines Not Lying On The Same Side Make The Adjacent Angles Equal To Two Right Angles, Then The Straight Lines Will Be In A Straight Line With Each Other-
For with straight line AB and point B lying upon it...
...let two straight lines BC and BD be made, both of which do not lie upon the same side (of AB)...
...and so make the adjacent angles ABC and ABD...
...which are equal to two right angles.
I say that BD is in a straight line with CB.
For if BD is not in a straight line with BC, then let straight line BE be drawn from CB.
If so, then straight line AB stands upon "straight line CBE", and therefore the two angles at ABC and ABE are both right angles. And then the angles ABC and ABD are also equal to right angles. Therefore, angles CBA and ABE are equal to CBA and ABD. Let the angle in common between the two, CBA, be removed: therefore, the remaining angle ABE is equal to the remaining angle ABD -- this is absurd, as the smaller does not equal the greater. Therefore, BE and CB are not in a straight line with each other, and likewise can be demonstrated that no other can be in a straight line except for BD. Therefore, BD is in a straight line with CB.
-Therefore, If With Any Straight Line And At Any Point On Said Straight Line Two Straight Lines Not Lying On The Same Side Make The Adjacent Angles Equal To Two Right Angles, Then The Straight Lines Will Be In A Straight Line With Each Other-
THE VERY THING WHICH HAD TO BE DEMONSTRATED
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις I'E' - Proposition the Fifteenth-
-If Two Straight Lines Bisect Each Other, They Make Vertical Angles Equal To Each Other-
For let straight line AB and BD bisect each other at point E...
For since straight line AE stands upon straight line CD, thus making angles CEA and AED, therefore, the angles CEA and AED are both equal to right angles. Again, since straight line DE stands upon straight line AB, thus making angles AED and DEB, therefore angles AED and DEB are both equal to right angles. And both angles CEA and AED have been demonstrated to be equal to right angles -- therefore, angles CEA and AED are equal to AED and DEB. Let the common angle AED be removed: the remaining angle CEA is equal to the remaining angle BED, and likewise shall it be demonstrated that also angle CEB and DEA are equal.
-Therefore, If With Any Straight Line And At Any Point On Said Straight Line Two Straight Lines Not Lying On The Same Side Make The Adjacent Angles Equal To Two Right Angles, Then The Straight Lines Will Be In A Straight Line With Each Other-
THE VERY THING WHICH HAD TO BE DEMONSTRATED
Πόρισμα: From This Is It Manifest That If Ever Two Straight Lines Bisect Each Other, They Will Make Angles At The Point Of The Section Equal To Four Right Angles.
Πόρισμα: From This Is It Manifest That If Ever Two Straight Lines Bisect Each Other, They Will Make Angles At The Point Of The Section Equal To Four Right Angles.
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις I'F' - Proposition the Sixteenth-
-For Every Triangle, With One Side Extended, The Exterior Angle Is Greater Than Either Of the Interior and Opposite Angles-
Let there be triangle ABC, and let one side of it, BC, be drawn out to point D.
I say that angle ACD which lies outside the triangle is greater than the interior and opposite angles, namely CBA and BAC.
...and let straight line BE connect points B and C, and let BE be drawn out to point F, and let straight line EF be equal to straight line BE.
And so, since AE is equal to EC, and BE to EF, then the two straight lines AE and EB are equal to CE and EF respectively. And the angle AEB is equal to angle FEC, for they vertically opposite.
Therefore, the base AB is equal to FC, and triangle ABE is equal to triangle FEC, and the remaining angles of one triangle are equal to the other triangle's remaining angles respectively, where the equal sides subtend.
Therefore, angle BAE is equal to angle ECF. The angle at ECD is greater than the angle ECF -- therefore, the angle ACD is greater than BAE; similarly, if BC be bisected, the angle BCG, which is in essence the same as angle ACD (via Prop. 15), is greater than ABC.
-Therefore, For Every Triangle, With One Side Extended, The Exterior Angle Is Greater Than Either Of the Interior and Opposite Angles-
THE VERY THING WHICH HAD TO BE DEMONSTRATED
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις I'Z' - Proposition the Seventeenth-
-For Every Triangle, Two Angles Summed Together In Any Way Are Less Than Two Right Angles-
Let there be triangle ABC: I say that two angles of triangle ABC summed together in any way are less than two right angles.
Let BC be extended out to point D.
And since angle ACD is an exterior angle, it is greater than the interior and opposite angles of triangle ABC (Prop. 16). Let angle ACB be added to each: therefore, angles ACD and ACB are greater than angles ABC and BCA. But the angles at ACD and ACB are equal to two right angles (Prop. 13). Therefore, the angles ABC and BCA are lesser than two right angles. In a similar fashion we can prove that the angles BAC and ACB are less than two right angles, as well as CAB and ABC.
And since angle ACD is an exterior angle, it is greater than the interior and opposite angles of triangle ABC (Prop. 16). Let angle ACB be added to each: therefore, angles ACD and ACB are greater than angles ABC and BCA. But the angles at ACD and ACB are equal to two right angles (Prop. 13). Therefore, the angles ABC and BCA are lesser than two right angles. In a similar fashion we can prove that the angles BAC and ACB are less than two right angles, as well as CAB and ABC.
-Therefore, For Every Triangle, Two Angles Summed Together In Any Way Are Less Than Two Right Angles-
THE VERY THING WHICH HAD TO BE DEMONSTRATED
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις I'H' - Proposition the Eighteenth-
-For Every Triangle, The Greater Side Subtends The Greater Angle-
For let there be triangle ABC, and it has one side, AC, larger than another side, AB. I say that the angle at ABC is larger than the angle at BCA.
For since side AC is larger than side AB, let side AD be found on side AC equal to AB.
Let points B and D be joined by line BD.
And since the angle at ADB is an angle exterior to triangle BCD, it is greater than the interior angle of that triangle and that triangle's opposite angle DCB (Prop. 16), and the angle ADB is equal to the angle ABD, since side AB is equal to side AD (Prop. 5): therefore, the angle ABD is greater than angle ACB, and so angle ABC is much greater than angle ACB.
Let points B and D be joined by line BD.
And since the angle at ADB is an angle exterior to triangle BCD, it is greater than the interior angle of that triangle and that triangle's opposite angle DCB (Prop. 16), and the angle ADB is equal to the angle ABD, since side AB is equal to side AD (Prop. 5): therefore, the angle ABD is greater than angle ACB, and so angle ABC is much greater than angle ACB.
-Therefore, For Every Triangle, The Greater Side Subtends The Greater Angle-
THE VERY THING WHICH HAD TO BE DEMONSTRATED
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις I'Θ' - Proposition the Nineteenth-
-For Every Triangle, The Greater Angle Subtends The Greater Side-
For let there be triangle ABC, and it has one angle, ABC, larger than another angle, BCA. I say that the side AC is larger than the side AB.
For if this were not true, then side AC has to be either equal or smaller than side AB. But, AC is not equal to AB, for then the angle at ABC would be equal to the angle at ACB (via Prop. 5), but this is not so. Therefore, side AC is greater than AB. Nor indeed is side AC smaller than side AB, for the angle at ABC would have to be smaller than ACB (via Prop. 18), but this is not so. Therefore, side AC is not smaller than side AB. And it hath also been shown that they are not equal either; therefore, side AC is larger than side AB.
-Therefore, For Every Triangle, The Greater Angle Subtends The Greater Side-
THE VERY THING WHICH HAD TO BE DEMONSTRATED
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις K' - Proposition the Twentieth-
-For Every Triangle, Two Sides Summed Together In Any Way Are Larger Than The Remaining Side-
Let there be triangle ABC. I say that two sides of triangle ABC summed together in any way are larger than the remaining side: that is, the sum of side BA and side AC are larger than side BC; the sum of side AB and side BC are larger than side AC; and the sum of side BC and side CA are larger than side AB.
For let side BA be drawn out to point D, and let line AD be labelled, equal to side CA. Then let line DC join D and C.
Now, since side DA is equal to AC, the angle at ADC is equal to the angle at ACD (via Prop. 5). Therefore, the angle at BCD is larger than the angle at ADC. And since DCB is a triangle having the angle BCD larger than the angle at BDC, and the larger angle subtends the larger side (via Prop. 18/19), then therefore side DB is larger than side BC. And side DA is equal to side AC, so therefore the sum of side BA and AC is larger than BC. Likewise we shall show that the sum of sides AB and BC are larger than side CA, and also the sum of sides BC and CA are larger than AB.
-Therefore, For Every Triangle, Two Sides Summed Together In Any Way Are Larger Than The Remaining Side-
THE VERY THING WHICH HAD TO BE DEMONSTRATED
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις K'A' - Proposition the Twenty-First-
-If Two Straight Lines Are Constructed Starting From The Opposite Ends of a Line Which Forms The Base Of Two Triangles, Where Said Two Lines Meet At A Point Within The Outer Triangle, Then The Two Lines Of This Inner Triangle Will Be Less Than The Remaining Two Sides Of The Outer Triangle, But The Inner's Angle Will Be Larger Than The Outer's Angle-
For let there be triangle ABC, and, from the ends of side BC, at points B and C, let two lines be constructed, meeting at point D within outer triangle ABC, thus forming sides BD and CD. I say that, while BD and CD are smaller than the other two sides of the outer triangle, sides AB and AC, angle BDC is larger than angle BAC.
For let BD be extended to point E, which lies upon AC. And since for every triangle the sum of two sides are larger than the third remaining side (via Prop. 20), then the two sides of triangle ABE, AB and AE, are larger than BE. Let CE be added to both; therefore, AB and AC are larger than BE and CE. And again, since the sum of two sides of triangle CDE, CE and DE, are larger than the remaining side CD; now let BD be added to both. Therefore, sides CE and BE are larger than CD and BD.
So, sides AB and AC hath been shown to be larger than BE and CE. Therefore, sides AB and AC are much larger than BD and CD.
Again, since for every triangle any exterior angle is larger than the two opposite angles (via Prop. 16), then for triangle CDE, the angle BDC is larger than angle CED. Moreover, by the same reasoning, CEB is an exterior angle to triangle ABE, and thus is larger than angle BAC. But angle BDC has already been shown to be larger than angle CEB, and therefore, angle BDC is much larger than angle BAC.
For let BD be extended to point E, which lies upon AC. And since for every triangle the sum of two sides are larger than the third remaining side (via Prop. 20), then the two sides of triangle ABE, AB and AE, are larger than BE. Let CE be added to both; therefore, AB and AC are larger than BE and CE. And again, since the sum of two sides of triangle CDE, CE and DE, are larger than the remaining side CD; now let BD be added to both. Therefore, sides CE and BE are larger than CD and BD.So, sides AB and AC hath been shown to be larger than BE and CE. Therefore, sides AB and AC are much larger than BD and CD.
-Therefore, If Two Straight Lines Are Constructed Starting From The Opposite Ends of a Line Which Forms The Base Of Two Triangles, Where Said Two Lines Meet At A Point Within The Outer Triangle, Then The Two Lines Of This Inner Triangle Will Be Less Than The Remaining Two Sides Of The Outer Triangle, But The Inner's Angle Will Be Larger Than The Outer's Angle-
THE VERY THING WHICH HAD TO BE DEMONSTRATED
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις K'B' - Proposition the Twenty-Second-
-Out Of Three Straight Lines Which Are Equal To Three Given Straight Lines, A Triangle Is Constructed, And It Is Necessary That Two Of The Straight Lines Summed Together In Any Way Be Greater Than The Remaining Side-
Let three given straight lines be called A, B, and C, and let two of these lines summed in any way be greater than the last remaining, so that A and B are greater than C, A and C are greater than B, and B and C is greater than A. So, it is necessary to set up a triangle out of lines equal to A, B, and C.
Let straight line DE be drawn, ending at point D, but stretching unending to point E...
and (using Prop. 3) let DF be drawn equal to line A...
...FG equal to B...
...and GH equal to C.
With center at point F, and diameter DF, let the circle DKL be drawn.
Likwise let circle HKL be drawn with center G and diameter GH.
Then let KF and KG be joined. I say that triangle KFG has been constructed out of the straight lines equal to A, B, and C. For, since point F is the center of circle DKL, DF is equal to FK, but DF is also equal to A. And again, since point G is the center of circle LKH, GH is equal to GK, but GH is also equal to C. Therefore, GK is also equal to C, and FG is equal to B. And so, the three straight lines KF, FG, and GK are equal to A, B, and C respectively.
-Therefore, Out Of Three Straight Lines KF, FG, And GK, Which Are Equal To Three Given Straight Lines A, B, And C, A Triangle KFG Is Constructed-
THE VERY THING WHICH HAD TO BE DONE
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις K'Γ' - Proposition the Twenty-Third-
-On A Given Straight Line And At A Point Lying On Said Line A Rectilinear Angle Equal To A Given Rectilinear Angle Is To Be Constructed-
Let a given straight line be called AB with point A lying on it, and let be given rectilinear angle called DCE.
It is necessary that on given straight line AB and at point A lying on said line, a rectilinear angle be constructed equal to given rectilinear angle DCE.
Let points D and E be taken at random on straight lines CD and CE respectively, and then let D and E be joined by line DE.
Then, using three straight lines equal to lines CD, DE, and CE (using Prop. 3), let triangle AFG be constructed so that CD is equal to AF, CE to AG, and DE and FG.
And since the two sides CD and CE are equal to AF and AG respectively, and base DE is equal to FG, then angle DCE is equal to angle FAG (Prop. 8).
-Therefore, On Given Straight Line AB And At Point A Lying On Said Line Given Rectilinear Angle FAG Equal To Given Rectilinear Angle DCE Has Been Constructed-
THE VERY THING WHICH HAD TO BE DONE
~~~~~~~~~~~~~~~~~~~~~~~
Προτάσις K'Δ' - Proposition the Twenty-Fourth-
-On A Given Straight Line And At A Point Lying On Said Line Rectilinear Angle FAG Equal To Given Rectilinear Angle DCE Has Been Constructed-
Let
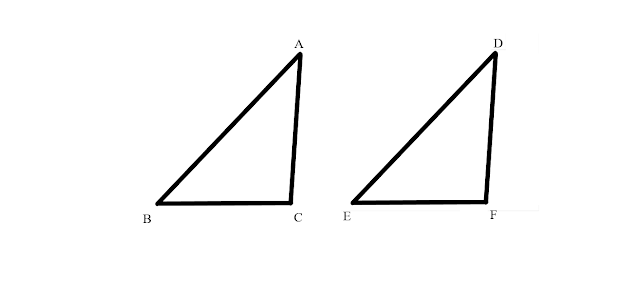
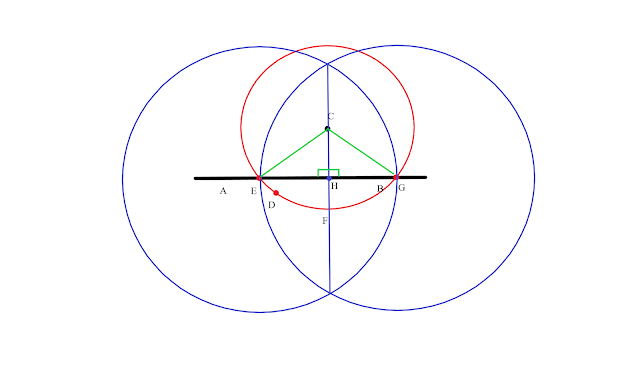
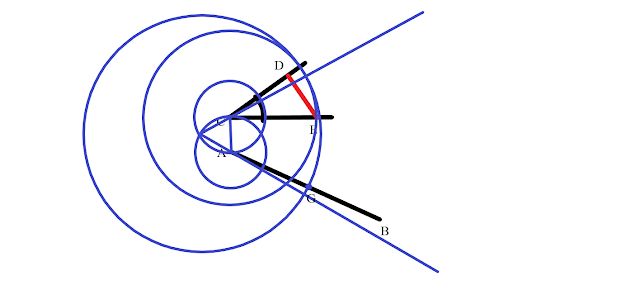
No comments:
Post a Comment